结构非线性仿真分析3个知识点

结构非线性分析用于研究结构在受到超过线性范围的负载时的行为，结构非线性分析主要涉及材料非线性、几何非线性和边界条件非线性等因素的研究，这些因素可能导致结构在不同加载条件下表现出不同的力学行为。这里分享3个知识点，具体如下：

01 材料非线性

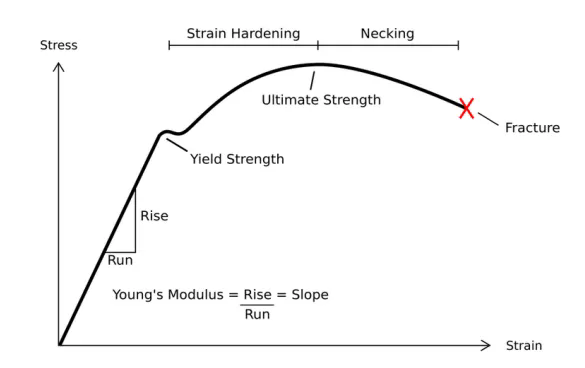
塑性变形：当材料应力超过一定限度时，会产生不可恢复的塑性变形。这种非线性行为对于设计像金属构件这样的结构至关重要，因为它们可能在极限状态下工作，如汽车在碰撞过程中的变形。

超弹性：某些材料（如橡胶）在经历大应变后能够完全恢复形状，这种超弹性材料的非线性特性对诸如密封件和隔震部件的设计十分重要。

02 几何非线性

大变形效应：在很多结构中，尤其是细长构件或柔软结构，自身位移可能非常大，足以改变结构的几何形状，这时需采用几何非线性分析方法来准确模拟其行为。

失稳与屈曲：结构在受到压缩力或压力作用时可能会发生失稳或屈曲，例如高层建筑在风载作用下的稳定性分析就需考虑几何非线性效应。

03 边界条件非线性

接触问题：当两个或多个结构之间存在接触时，其边界条件会随着加载而变化，导致复杂的非线性行为。例如，螺栓连接和齿轮啮合中的接触分析对预测结构的功能和耐久性至关重要。

摩擦滑动：接触表面间的摩擦力可以导致复杂的动态行为，如刹车系统和地震中建筑物基础与土壤之间的相互作用。

结构非线性问题可归结为非线性方程的求解，其求解方法有很多种，如牛顿法、简化的牛顿法、牛顿迭代法等。在进行结构非线性分析时，求解过程可能遇到不收敛的问题，这常常需要通过调整求解器设置或改进模型来实现。例如，使用牛顿-拉弗森方法进行迭代求解时，需要仔细选择初始步长和收敛准则。

为了确保计算结果的准确性，需要实时监控求解过程中的残差和其它关键指标，以便及时发现并纠正可能的问题。