仿真过程中单元合理选取高级精髓

当前市场商业化仿真软件已经遍地开花，但其都是基于有限单元法理论，这就要求我们仿真工程能够对有限元单元法理论要完全掌握。另外在我们实际仿真工作过程中，存在一个比较大的缺陷，仿真工程师在对结构离散过程中，忽视了对单元的合理选择及单元选择对仿真精度影响，因此本文重点对因单元选择引起的误差进行说明，以问答的方式进行阐述，使仿真工作者能够对因单元引起的结果偏差找到原因、解决方法。

沙漏模式：

哪种单元出现：线性减缩积分单元的应力/位移场分析中；

何为沙漏模式：因线性减缩积分单元积分点较少，可能出现没有刚度的零能量模

式（沙漏模式），网格较粗时，零能模式会通过网格扩展出去，

是计算结果无意义；

判断：

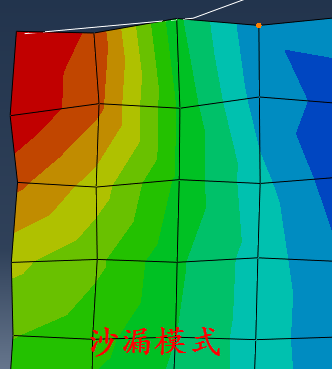
方法1：查看单元的变形情况，如果单元变成交替出现的梯形形状，就可能出现沙漏模式，如下图：

方法2：result-history output，绘制ALLAE（伪应变能）和内能ALLIE曲线，

ALLAE占ALLIE的1%时，表明沙漏模式对计算结果影响不大；超过10%

时，分析认为无效。

沙漏控制：

沙漏控制：abaqus中的伪应变能或沙漏刚度主要用来控制沙漏变形能量；

措施：

l  细化网格：线性减缩积分单元要避免过于粗糙的网格，如结构发生弯曲变形，则在厚度方向上至少划分4个单元；

l  设置沙漏控制：引入少量的人工“沙漏刚度”来限制沙漏模式的扩展。网格足够细化时，方法非常有效，可获得足够精确的计算结果。enhanced、relax stiffness、stiffness、viscous、combined。

Ø  沙漏控制时，所设置的沙漏控制选项数值大于默认值，可能导致沙漏刚度过大而出现数值不稳定；

Ø  一般采用默认，默认出现沙漏模式，往往是由于网格太稀疏，最好修改网格。

l  选择其他单元类型：非协调单元不会出现沙漏模式问题，适用于abaqus/standard各种分析；

l  避免将载荷或边界条件只定义在一个节点上。将点载荷或点上的边界条件定义在一个包含该点的小区域上，有利于避免沙漏模式的扩展。

剪切自锁：

定义：单元的位移场不能模拟由于弯曲而引起的剪切变形和弯曲变形；

何时出现：弯曲变形的线性完全积分单元中出现；

原因：

n  线性单元的直边不能承受弯曲载荷作用，分析过程中可能出现本来不存在的虚假剪应力，是单元的弯曲刚度过大，计算的位移值偏小；

n  二次单元的边可发生弯曲，一般不会出现剪切自锁现象。（单元畸变非常

严重，或应力状态非常复杂，存在弯曲应力梯度，二次单元也会出现某种程度的闭锁现象）。

特点：剪切自锁仅影响受弯曲载荷作用的完全积分线性单元；

措施：考虑采用非协调单元或减缩积分单元。

体积自锁：

定义：完全积分单元受到过度约束时的一种闭锁现象；

特点：如果材料是不可压缩的或近似于不可压缩，完全积分单元可能变得特别刚

硬而不产生体积变形；

评判：各个积分点之间或各个单元之间的静水压力出现急剧变化；（后处理中绘

制静水压应力云纹图，突变，呈棋盘形分布，有可能出现体积自锁。）

措施：

l  合适单元类型：杂交

l  细化网格：塑性应变较大的区域划分足够细化的网格；