有限元仿真分析方法中计算的误差来源与处理方法

 有限元法是一种高效能、常用的数值计算方法。科学计算领域，常常需要求解各类微分方程，而许多微分方程的解析解一般很难得到，使用有限元法将微分方程离散化后，可以编制程序，使用计算机辅助求解。

 深圳市有限元科技有限公司是一家有十年有限元分析项目经验的高科技企业，公司代理国外多款着名有限元软件，并提供软件的销售与培训业务，另研发出多款行业有限元通用软件，并秉承以最高质量的产品和最高质量的服务满足客户的各种需求的服务理念，致力于为客户提供一站式有限元整体解决方案，目前已为全国超过500家企业提供有限元分析服务。如需购买有限元软件或咨询服务请联系电话：13632683051，咨询QQ：4006046636。

 在有限元计算中，用户最关心自己计算的结果是否准确与合理，那么今天有限元科技小编就和大家谈谈有限元计算的误差来源。

 按照误差来源类型主要分为两类：

 1、有限元理论假设引入的误差

 限元这种数值计算方法，为了实现对现实问题的计算，引入一些力学假设，即

 （1）连续介质假设，认为计算模型是理想连续，没有孔洞，即位移具有单值性，但是实际产品在加工中难以避免会引入初始的孔洞缺陷，例如铸造件。

 （2）材料均匀性假设，www.featech.com.cn认为模型的材料参数不随空间变化为变化，是均匀的，但是实际产品在工艺处理过程中，例如淬火，都会使得材料的力学性能发生改变，并不能严格满足材料均匀性。有限元理论与真实物理世界的差别通过一个系数来进行折中，也就是有限元计算得到一个基准结果，再通过实验进行对比，计算得到二者的转换系数。

 2、有限元计算过程的误差

 有限元的计算过程主要包括前处理，求解和后处理三个阶段，有限元计算过程的误差主要发生在前处理和求解阶段。

 第一个误差来源，即模型简化，发生在前处理阶段模型简化的是否恰当直接影响的计算结果，一般情况数值计算模型与产品的加工CAD模型还是有区别的，数值计算模型只要求把模型的主要特征反映出来，而舍去一下细致的特征，从而平衡了求解精度与计算效率。

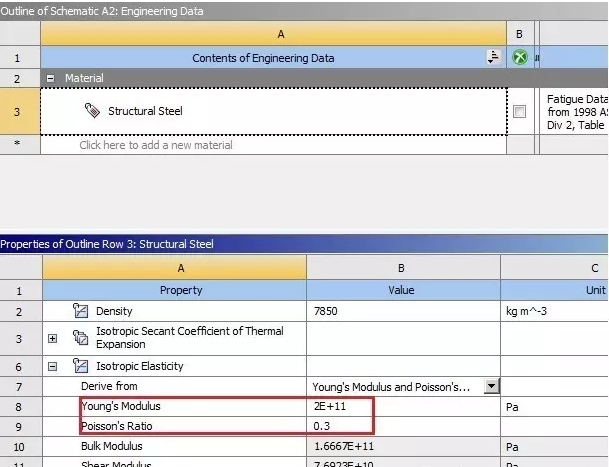
 第二个误差来源，即材料参数，就是反映计算模型的材料参数，如弹性模量，泊松比等，但是如前所述，即使找到材料参数也不能完全反应由于工艺造成的材料非均匀性，如果输入了错误的材料参数，则计算得到结果没有价值。

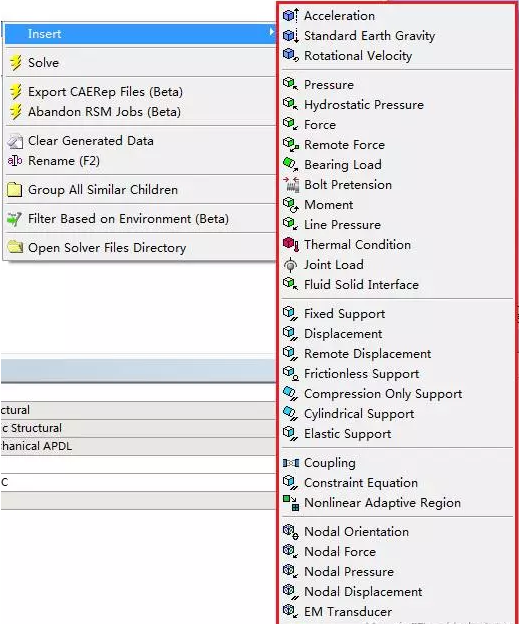
 第三个误差来源，即工况对接，所谓工况对接，就是在软件中设置的位移约束和载荷与模型实际工况的对应情况，软件只提供了有限的位移约束和载荷类型，www.featech.com.cn而分析模型可能收到的约束和载荷非常多，如果二者对应不正确，则计算结果也没有价值。

 第四个误差来源，即网格划分，这个大家容易理解，也是目前很多文献提到的比较多的一个误差，要想将该误差降到最低，必须通过合理的网格加密得到网格无关解。

 3、总结与处理

 有限元理论假设引入的误差是有限元理论与生俱来的，无法避免只能通过一些实验数据进行修正，这也说明要想有限元对工程设计产生作用，必须有与实验对比的过程。有限元计算过程的误差是我们可以控制和降低的，在这四个误差来中，一到三决定了分析问题的本质，第四个误差来源只是影响计算精度，在以上四种误差来源中，材料参数相对好处理，只要找到合理的材料数据即可，剩下的误差，都需要软件使用者具有丰富的工程与软件使用经验才可以降低。

 本文出自深圳有限元科技有限公司官网：www.featech.com.cn 转载请注明