材料力学笔记之——应力集中与应力奇异

应力集中

从以上的分析来看，应力集中通常出现在构件空间发生突变，空间曲率或梯度发生改变的位置；若过渡区域不光滑连续，则可能会出现应力奇异。由此，构件内应力集中现象与构件空间的性质相关，对于应力集中的原因从“场”的观点来解释或许会更为恰当。力或应力在空间中的传递过程中所形成的“场”与流体相似。在“传递”或“流经”的路径上，空间性质的改变将会使其产生调整，并重新分布。目前尚未查阅到深入探讨相关相似问题的文献，但相信这可能会很有趣。如果将这种应力集中的局部现象推广到宇宙空间，会是什么样的区域存在“应力集中”呢？“应力集中”区域会有哪些奇观呢？

出现应力集中的区域

通过研究得出：

• 材料夹杂与基体弹性模量的差异越大，产生的局部应力集中也越大，气孔导致的应力集中大于硬夹杂；

  
  

• 多个夹杂存在时，相邻的应力场会发生耦合强化作用，强化效果与夹杂排列方向和加载方向有关；

  
  

• 在忽略夹杂的循环塑性条件下，循环应力对气孔周围应力集中影响较大，但对硬夹杂周围应力集中影响很小；

  
  

• 气孔非常靠近表面时，应力水平越高，应力应变集中系数Kg越大，裂纹容易在表面萌生。气孔的位置较深时，应力水平越低，Kg越大，裂纹容易在内部夹杂处萌生。

应力集中的影响

对于脆性材料，应力集中处的应力达到比例极限后材料开始破坏。通常裂纹是在应力集中处形成，然后更大的应力集中将产生于裂纹尖端处，这反过来引起裂纹在该截面的进一步扩展，导致材料的突然断裂。

对于塑性材料，并承受静态载荷时，细小的几何缺陷、划痕、小圆角等不需要过于担心，设计者通常忽略应力集中系数的影响。因为此时应力超过材料比例极限并不会导致裂纹产生。反而，由于屈服和应变强化的影响，材料还有进一步承载的能力。但在动载荷或交变载荷作用下，应力集中部位是疲劳裂纹的重要发源地，降低构件的疲劳寿命。

1. 圆角

轴的圆角半径r 与疲劳极限σ-1 之间的关系是：随着圆角半径r 减小，直径d 增大，疲劳缺口应力集中系数急剧增大；反之则反。据我国某拖拉机厂统计分析了180根曲轴的疲劳断裂案例，发现大多数断裂时有与大修时轴径磨削使轴径的圆角半径小于设计规定 (r=6) 所致，其中圆角r=1.5~3的断轴率为70.8%，r=3~4的占18%，r=4~5的占4%[14]。

2. 纵向沟槽

如键槽和花键等轴上的纵向沟槽，是承受扭转应力轴件的常见失效发源地。这类失效大多数发生在尖角处，因为应力集中而萌生小裂纹造成疲劳断裂。分析表明，键槽尖角引起的局部应力可达到平均额定应力的十倍。

3. 孔

轴类零件开一横孔后，孔内侧的理论应力集中系数Kt 随着d/D 比值的上升而距离增大(d，横孔直径；D 为轴向直径)。

4. 受内压壳体开孔接管处的应力集中

压力容器接管处的应力集中较小孔严重的多，应力集中系数可达到3~6，但其应力衰减迅速，具有明显的局部性，不会使壳体引起任何显著的变形，故可以允许应力峰值超过材料的平均屈服应力。

5. 椭圆孔

椭圆孔无限大板，在其均匀应力垂直于椭圆长轴的情况下，最大应力发生在椭圆孔的长轴端点处，应力集中系数为Kt=1+2a/b。

6. V型缺口尖端ρ→0时

形成一个尖锐缺口，在拉伸应力作用下，缺口尖端的应力趋于无限大，将出现所谓的奇异性。缺口尖端局部区应力可以表示为：σij∝r -1+λ；λ 为奇异指数，λ 与V 形缺口角β 有关，当β=180°时，λ=1，无缺口情况；当β＜180°时，λ 总小于1，当r →0时，缺口尖端应力具有奇异性；β=0.5时，缺口转化为裂纹，λ=0.5时，即裂纹尖端的应力奇异指数为0.5。

7. 重复缺口

重复缺口效应是指，两个或两个以上的应力集中因素互相重叠而使应力集中进一步加剧的现象，如图1所示。如果应力集中因素Ⅱ的作用远小于应力集中因素Ⅰ的作用，则二重应力集中因素KⅠ,Ⅱ=KⅠKⅡ；如果应力集中因素Ⅱ的作用远超过应力集中系数Ⅰ，则缺口效应主要取决于应力集中因素Ⅱ。

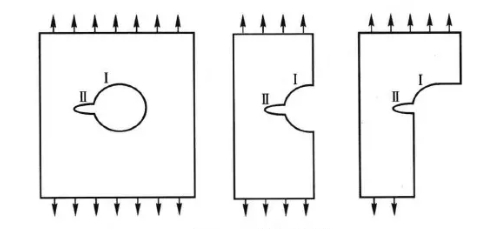
图1 重复应力集中

8. 熔焊接头

在熔焊接头中，焊缝与母材的过渡处（焊趾）产生应力集中。焊趾是焊接接口中的典型缺口，其缺口应力可以分解为平均应力σm、弯曲应力σb 和非线性应力σp。对接接头应力集中系数的大小，主要取决于焊缝余高和焊缝向母材的过渡圆弧半径及夹角，增加余高和减小过渡圆弧半径，都会使应力集中系数增加。T形（十字）焊接接头焊缝向母材过渡较急剧，其工作应力分布极不均匀，在角焊缝的根部和焊趾都存在严重的应力集中。

搭接焊缝在只有正面焊缝的搭接接头中，工作应力分布极不均匀，在角焊缝根部和焊趾处都有严重的应力集中。在用侧面焊缝联接的搭接接头中，其工作应力更为复杂。各种焊接接头焊后都存在不同程度的应力集中，应力集中对接头强度的影响与材料性能、载荷类型和环境条件等因素有关。如果接头所用材料有良好的塑性，接头破坏前有显著的塑性变形，使得应力在加载过程中发生均匀化，则应力集中对接头的静强度不会产生影响。

点焊焊接接头应力集中程度比电弧焊搭接接头的应力集中程度严重，点焊接头承受载荷时，其焊点周围产生不同程度的应力集中，点焊接头的抗拉强度明显低于抗剪强度，所以在一般使用中，应尽量避免点焊接头承受图2所示载荷。焊接节点部位由于传力方向改变产生复杂的结构应力，结构应力与节点焊缝的应力集中互相叠加。焊接节点的应力集中分析是焊接结构强度设计中需要考虑的重要因素，焊接缺陷是焊接结构中最严重的不完整性，对焊接结构承载能力有显著的影响，并在缺陷周围产生应力集中。

图2 点焊承受的载荷及应力分布

应力集中与圣维南原理

圣维南原理所描述的局部效应与应力集中存集聚之处，都是应力、应变的局部效应，但也有所区别。圣维南原理主要描述的是边界条件等效所引起的局部应力，应变误差的影响问题；而应力集中则主要探讨构件空间突变所引起的应力集中问题。圣维南原理是在计算求解力学问题时的一个边界简化假设依据，且描述相对模糊；而应力集中则是力学求解的一种结果，且应力集中的局部特性可以进行量化描述。

关于矩形板、圆形开孔的孔边应力集成程度与距离圆孔中心远近的关系，即一矩形薄板，在离开边界较远处有半径为a 的小圆孔，左右两侧受局部拉力，集度（内应力）为q，通过分析得出，应力在孔边 (ρ=a) 是无孔时的3倍；ρ=2a 时为1.22q；ρ=3a 时为1.07q；ρ=4a 时为1.04q。

图3 带圆孔矩形薄板应力集中问题

应力集中系数

1. 拉伸应力集中系数

理论应力集中因素等于应力集中处的最大应力σmax 与该界面的平均应力σnom 的比，即K=σmax/σnom。其中，σnom=FN/A，A 是考虑截面削弱后的横截面面积，称为净面积；有时平均应力的计算可以不考虑截面的削弱。理论应力集中系数K 始终大于1。对于板宽超过孔径4倍的板条，理论应力集中因素K≈3。

2. 扭转应力集中

在工程上为了避免在轴尺寸不连续处进行复杂的应力分析，最大切应力通常可根据特定的几何结构由一扭转应力集中系数K 确定，τmax=KTc/J。T 是截面上的合力矩，J 是截面极惯性矩，c 是轴的外半径。

3. 弯曲应力集中系数

σmax=KMc/I，K 是应力集中系数；M 是关于横截面中性轴的合内力偶矩，I 是横截面关于中心轴的惯性矩，c 是梁外表面到中性轴的垂直距离。

应力集中系数是基于静态加载给出的，并假设材料内部应力不能超过其本身的比例极限，材料是各向同性且均匀的。局部最大应力可以用弹性力学解析法、光弹法或有限元法求得，从而得到各种几何形状的试样在各种载荷下的理论应力集中系数。常见构件形状的应力集中系数曲线，可查阅机械设计手册[9]，但需要注意的是，不同的载荷和截面形式所对应的应力集中系数是不同的。

应力集中有限元求解的网格划分

有限元分析建模，网格划分时，对于不同部位的单元可以采用不同的大小，也应当采用不同的大小。对于边界比较曲折的部位是应力和位移变化的比较剧烈的部位，单元必须小一些；在边界比较平直的部位、次要部位以及应力和位移变化比较平缓的部位，单元可以大一些。当结构存在凹槽或孔洞时，在凹槽或孔洞附近将发生应力集中，即该处的应力较大且变化剧烈，必须把该处的网格划得较为紧密，以便更为贴切的描述此处的应力和应变的变化。对此，一般有两种方法：

由于应力集中区域的应力在结构强度分析中的重要性。因此，获得精准、稳定、可靠的解至关重要。在有限元分析中，则是要消除离散误差，获得网格无关解。离散误差的大小同离散方程的截断段误差有关。在相同的网格步长下，一般来说随着截断误差阶数提高，离散误差会逐渐减小。

对于同一离散格式，网格加密，离散误差也会减小。在实际计算中，应使得网格细密到即使再进一步细化网格，在工程允许的误差范围内数据值解也几乎不再发生变化，此时的解则认为是网格无关解。目前大多数有限元软件都是采用“位移法”进行求解，其中通过虚功原理和最小作用原理，最先求解的未知量就是位移。因而，若在随着网格逐步精细化的过程中，位移结果收敛于一个有限值，而应力则是发散的，出现此类情况也可以判断此处出现了应力奇异。

应力集中的预防与利用

下面是在结构设计中，避免应力集中的一些基本措施：

• 避免零件两交接部位的截面尺寸相差太大；

  
  

• 增大零件上过渡曲线的曲率半径，比如加大轴径变化处的圆角半径；

  
  

• 降低承受冲击载荷零件的刚度；

  
  

• 加大压配合部分轴的尺寸或开卸载槽；

  
  

• 焊接结构件要避免将焊缝布置在应力集中处，对于动载荷结构尤应注意。

  
  

• 合理设置筋板、肋板，分散或转移应力集中。

应力集中虽然对于承载结构来讲存在不利影响，但正是由于应力集中效应，为一些功能的实现起到重要作用。比如，食品袋上的缺口，可以方便食用时撕开；易拉罐拉片周围的压痕所产生应力集中，以方便开罐，等等。这些有效利用应力集中效应的实际案例，对于在使用中需要破坏和去除的结构来讲是有利的。

应力奇异与判断

根据弹性理论在结构内部尖角处，或说非光滑连续处的应力是无限大。在使用有限元求解过程中，应力奇异具有以下特点：

在有限元计算分析实践中发现，应力奇异的区域应力集中系数较高，理论上是无限大，应力集中度会很高，应力衰减明显。因此在分析中，首先需要关注的是结构上那些不光滑连续的区域；其次，对不连续区域的邻域进行划分，并在网格细化，寻找网格无关解的过程，比较确认不同区域计算值的收敛程度。当不连续区域邻域内的解已趋于收敛，且满足误差要求，但不连续区域的解始终差异较大时，就可以确认该区域出现了应力奇异。

应力奇异处理

在遇到应力奇异时，可以考虑采用以下方法进行处理：

• 细化模型。主要是在模型中添加细节特征（如倒角、过渡面等），再重新计算或者采用子模型法进行分析。

  
  

• 外插值法或路径法。假设应力奇异在该区域没有发生用来推断奇异点的应力值，可使用应力集中系数来计算真实应力。

  
  

• 局部细化网格。在几何尖角处，应力解梯度大的区域网格应细分，其他远离的位置可以粗划。如果远离奇异点的解是收敛的，则粗糙网格也会较为准确的估计这部分的解，但对于接近奇异点的解是不可靠的。

  
  

• 将模型转化为可借用理论公式计算的形式，并根据设计手册查找该模型结构及尺寸的应力集中系数来预测真实应力。

来源：产品设计研习社