CAE有限元法在形状优化方面的仿真应用

 形状优化一般分为基于几何参数的形状优化、基于形状基础向量的形状优化、非参数形状优化三种。下面，有限元科技小编给您分享CAE有限元法在形状优化方面的仿真应用。

 基于几何参数的形状优化几何参数的修改和CAD几何相关联，设计变量为半径、长度、角度等参数，且每次迭代后需要重新划分网格，其优化结果依赖于设计变量的选择数；

 基于形状基础向量的形状优化，有限元模型参数使用基础形状，需要优化系统找出用户定义基础形状的最优组合；

 而非参数形状优化需要每个节点可以从临近节点处独自移动，网格平滑算法确保网格质量，没必要使用敏度分析，优化可以使用标准的有限元求解器。

 基于几何参数的形状优化示意图及流程见图1、图2：

图1基于几何参数的形状优化

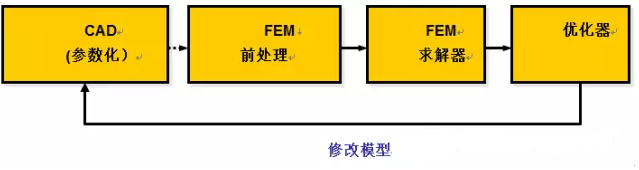
图2基于几何参数的形状优化流程

 其对设计变量选择性的依赖性可以从下述实例中看出：

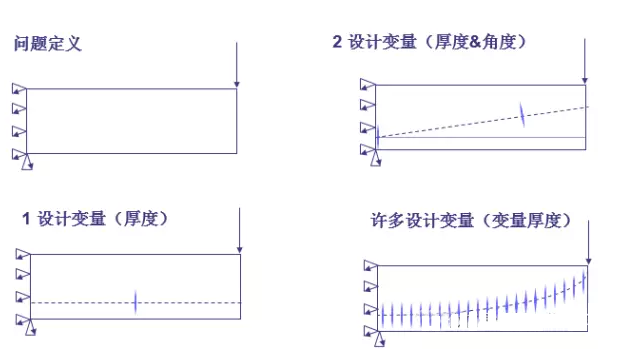
图3设计变量选择数的依赖性

 基于形状基础向量的形状优化的示意图及流程如图4、图5所示：

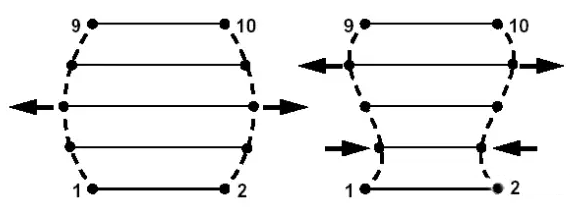
图4基于形状基础向量的形状优化

图5基于形状基础向量的形状优化流程

 下以一实例图6来说明参数形状优化：

图6参数形状优化

 非参数形状优化示意图及流程如图7、图8所示：

图7非参数形状优化

图8非参数形状优化流程

 下以一实例图9来说明非参数形状优化：

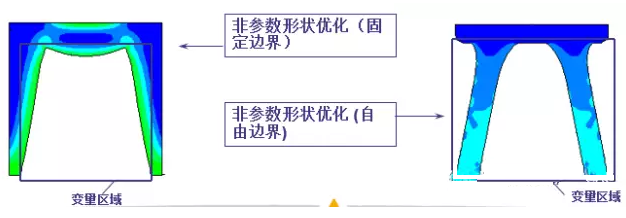
图9非参数形状优化

 从以上可以看出，使用非参数形状优化，对于设计变量有较低限制，效率高；而使用基于基于几何参数的形状优化、基于形状基础向量的形状优化对设计变量有较高限制，且效率不高。如下图10所示：

图10设计变量限制

 使用基于TOSCA软件的参数优化，可以得到更好的优化结果，应力幅大幅降低，迭代次数更少，如下图11所示：

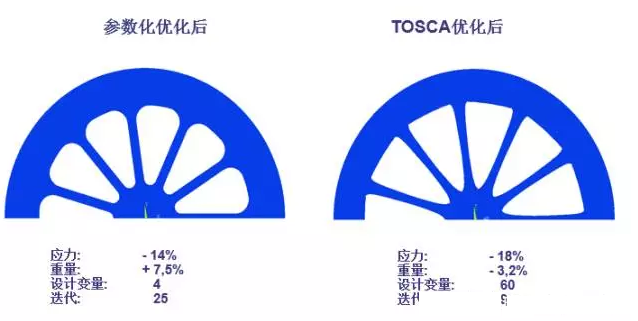
图11优化结果对比

 本文出自深圳有限元科技有限公司官网：www.featech.com.cn 转载请注明